プリコネRで考える確率

　日本では1月に共通テスト（旧共通一次/センター試験）が実施されます。大学受験の山場の時期です。そこで、少し役に立ちそうな記事を書いてみます。

• 題材としているゲームの関係者ではありません。一プレイヤーです。

要旨

背景

　プリコネR ¹は「ギルドハウス」という家具を自由に配置できるゲームシステムを備えています。なぜかは覚えていませんが、あるとき以下のようなパーティションで区切られた部屋を作りました。

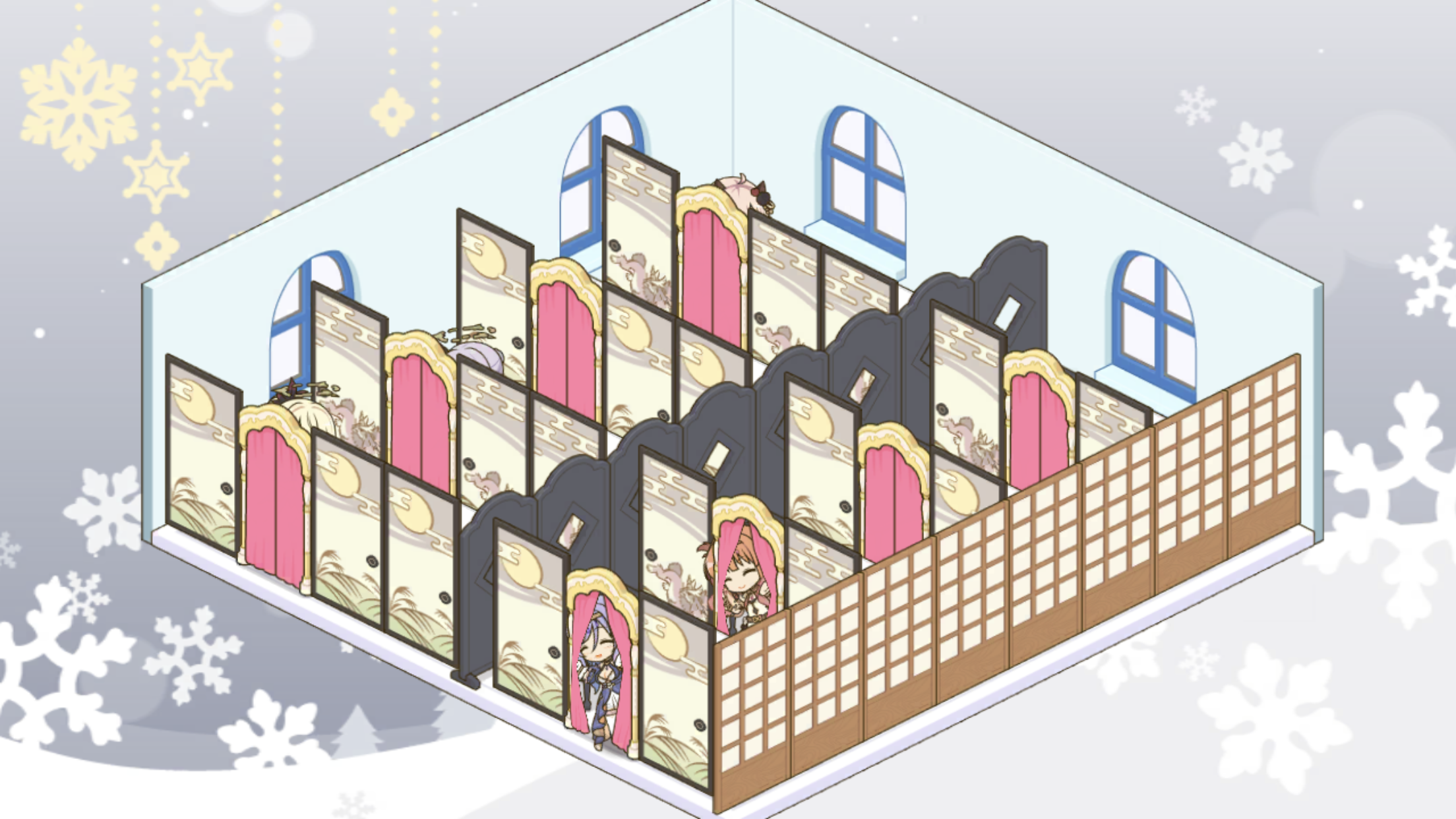
　しばらく運用していたところ、「8箇所ある割に二人のキャラクターが同じ箇所になることが多い」ことに気づきました。この謎を解明するためには確率を計算するしかありません。

1スペースに二人が入っている例

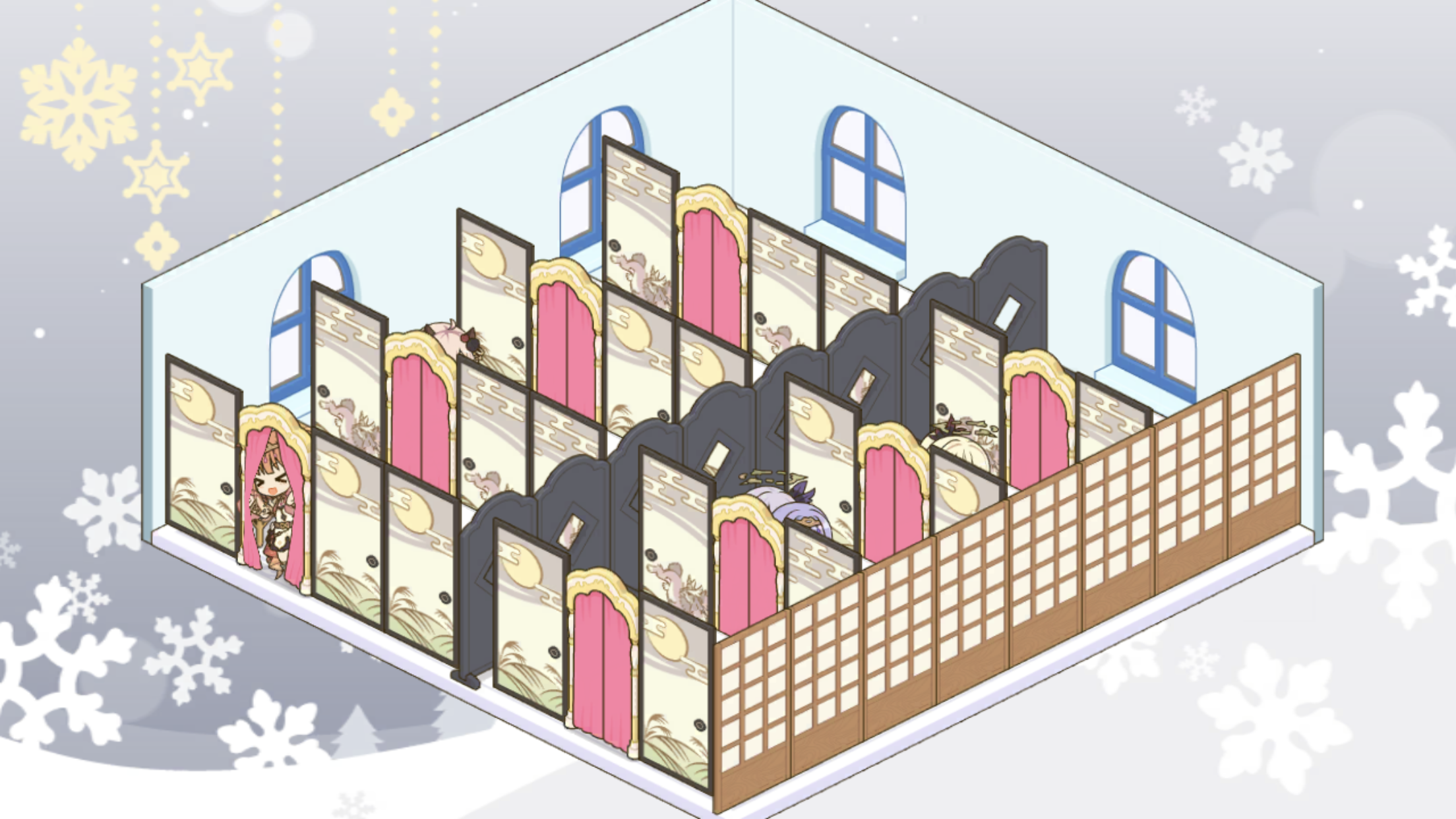
2スペースに二人が入っている例

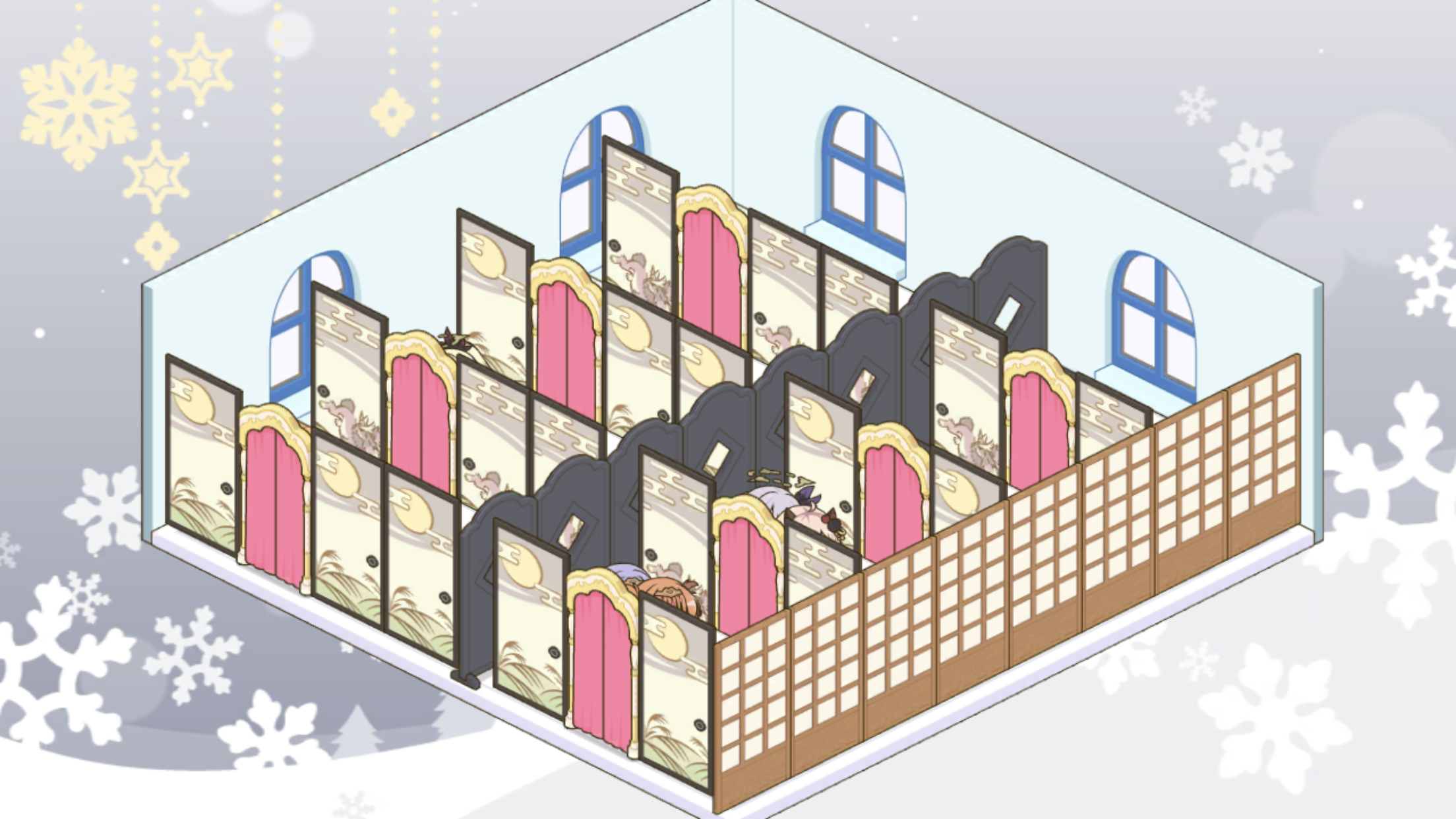
問題整理

受験問題に落とし込む前に状況を少し整理しておきます。

• 2マスのスペース²が8箇所ある
• キャラクターは5人配置する
• 部屋を開くたびに配置可能な場所にランダムに配置される
• 1スペースには最大で二人が配置される
• 5人なので、二人配置される箇所は最大でも2箇所

従って、問題は以下のようになります。³

リノ、シズル、リリ、クリア、イノリの5人を以下のギルドハウスに無作為に配置する。ギルドハウスには2マスの領域をもつスペースが8箇所ある。1名配置するためには1マスを要する。このとき、少なくとも2名が同じスペースに配置される確率を求めよ。

受験問題文例

　実際に目にする退屈な問題文は以下のようなものでしょうか。

　試験中にこのような問題を見かけた際にはギルドハウスを思い出してください。

「少なくとも」は余事象で考える

　「少なくとも」は、全体集合から余事象を引くことで目的とする集合を得ることができます。

$$ P(A) = P(U) - P(\bar{A}) $$

　本問題の場合は、

• 二人が同じ場所にいるスペースが1箇所ある
• 二人が同じ場所にいるスペースが2箇所ある

という複数の場合分けがあり、それぞれ考えることが若干面倒です。対して余事象は、

• 全員が異なるスペースにいる

という単一のケースなので、こちらを考えた方が楽そうです。

場合の数で考える

では、解いていきます。

■ 全部の通り

• 最初の一人は16箇所から選べる
• 二人目は15箇所から選べる
• 三人目は14箇所から選べる
• 四人目は13箇所から選べる
• 五人目は12箇所から選べる

$$ _{16}P_{5} $$

■ 全員が異なるスペースにいる

• 最初の一人は16箇所から選べる
• 二人目は先の一人と異なる場所にするために、14箇所から選べる
• 三人目は先の二人と異なる場所にするために、12箇所から選べる
• 四人目は先の三人と異なる場所にするために、10箇所から選べる
• 五人目は先の四人と異なる場所にするために、8箇所から選べる

$$ 16*14*12*10*8 $$

■ 場合の数の通りを全部の通りで割る

$$ \frac {16*14*12*10*8} {_{16}P_{5}} = \frac {\cancel{16}*\cancel{14}*\cancel{12}*^{2}\cancel{10}*8} {\cancel{16}*{_3}\cancel{15}*\cancel{14}*13*\cancel{12}} = \frac {16} {39} $$

これは五人全員が異なるスペースにいる余事象の確率です。

■ 1から引くことで知りたい確率を求める

$$ 1 - \frac {16} {39} = \frac {23} {39} = 0.589743 $$

どうやら58.97%は少なくとも二人は同じスペースになるようです。

組み合わせで考える

　本来、確率を考える場合にはすべての場合を区別して数え上げる必要があります。これは、本問題の場合は1スペースにつきそれぞれ2箇所の選択があり、組み合わせとしては同じスペースであっても区別して考える必要があります。しかし、順列と組み合わせが同様に確からしいといった条件を満たす場合に重複する場合を省いた状態で確率を求めることができます。

■ 全体の組み合わせ

• 全体の組み合わせは、16箇所から5カ所を選ぶ

$$ _{16}C_{5} $$

■ 全員が異なるスペースにいる

• 全員が異なるスペースとなる組み合わせは、8種類から5カ所を選ぶ
• それが、それぞれ2箇所ある

$$ _{8}C_{5}*2^{5} $$

■ 組み合わせの数を全体の組み合わせの数で割る

$$ \frac {_{8}C_{5}*2^{5}} {_{16}C_{5}} = \frac {\cancel{8*2}*\cancel{7*2}*\cancel{3*5}*\cancel{4}*16} {\cancel{16}*\cancel{15}*\cancel{14}*13*_{3}\cancel{12}} = \frac {16} {39} $$

場合の数と同じく、これは余事象で五人全員が異なるスペースにいる確率です。

■ 確率を求める

$$ 1 - \frac {16} {39} = \frac {23} {39} = 0.589743 $$

同じですね。

すべて列挙する

　受験向けではありませんが、確率の問題で現実的に数えられる通りの数であれば、すべてを列挙することも一つの手です。

本問題では、

• 場合の数で524,160通り
• 組み合わせの数で4,368通り

ですので不向きです。列挙は諦めます。

シミュレーションする

　受験向けではありませんが、大数の法則により、試行回数を稼ぐことでおおよその確率を知ることができます。以下にシミュレーションするためのPythonプログラムを乗せておきます。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

import random

# 1回の試行
def run_trial():
    # 1から8までのスペースがそれぞれ2箇所ずつ
    space = [number for number in range(1, 9) for _ in range(2)]

    # 5人の場所を無作為に選ぶ
    random.shuffle(space)
    chosen_charactors = [space.pop() for _ in range(5)]
    return len(set(chosen_charactors)) < 5  # 重複があるかチェック

# 全体の試行
def experiment(trials):
    # 重複がある試行の回数を数える
    duplicate_count = sum(run_trial() for _ in range(trials))
    return duplicate_count / trials

# 試行回数を設定
trials = 10000
experiment_result = experiment(trials)
experiment_result

　私が実行したときの結果は、「0.5897」でした。

観測する

　今回のケースでは、プログラムを書かずとも、実機で画面を開くたびに観測が可能な状況です。お暇な方は300回ほど試行してみるとおおよその結果が得られるでしょう。

　私が実行したときの結果は、370回の試行では219:151で「0.5919」でした。

まとめ

　「少なくとも二人が同じスペースになる確率は、約58.97%」という結果になりました。誕生日のパラドックスのように（私の）直感に反して意外と確率が高いようです。

　大学受験で解く類いの問題が如何に現実の問題と紐付き、役に立つのかをお伝えしたかった次第です。試験中にギルドハウスのことを思い出して、確率の問題を一人でも多くの人が解けることを願っております。